Draws plausible values based on test scores
Arguments
- dataSrc
a connection to a dexter database, a matrix, or a data.frame with columns: person_id, item_id, item_score
- parms
An object returned by function
fit_enormcontaining parameter estimates or a data.frame with columns item_id, item_score and, beta. If parms are provided, item parameters are considered known. If parms is NULL, they will be estimated Bayesianly.- predicate
an expression to filter data. If missing, the function will use all data in dataSrc
- covariates
name or a vector of names of the variables to group the populations used to improve the prior. A covariate must be a discrete person property (e.g. not a float) that indicates nominal categories, e.g. gender or school. If dataSrc is a data.frame, it must contain the covariate.
- nPV
Number of plausible values to draw per person.
- parms_draw
when the item parameters are estimated with method "Bayes" (see:
fit_enorm), parms_draw specifies whether to use a sample (a different item parameter draw for each plausible values draw) or the posterior mean of the item draws. Alternatively, it can be an integer specifying a specific draw. It is ignored when parms is not estimated Bayesianly.- prior_dist
use a normal prior for the plausible values or a mixture of two normals. A mixture is only possible when there are no covariates.
- merge_within_persons
If a person took multiple booklets, this indicates whether plausible values are generated per person (TRUE) or per booklet (FALSE)
Value
A data.frame with columns booklet_id, person_id, booklet_score, any covariate columns, and nPV plausible values named PV1...PVn.
Details
When the item parameters are estimated using fit_enorm(..., method='Bayes') and parms_draw = 'sample', the uncertainty
of the item parameters estimates is taken into account when drawing multiple plausible values.
In there are covariates, the prior distribution is a hierarchical normal with equal variances across groups. When there is only one group this becomes a regular normal distribution. When there are no covariates and prior_dist = "mixture", the prior is a mixture distribution of two normal distributions which gives a little more flexibility than a normal prior.
References
Marsman, M., Maris, G., Bechger, T. M., and Glas, C.A.C. (2016) What can we learn from plausible values? Psychometrika. 2016; 81: 274-289. See also the vignette.
Examples
db = start_new_project(verbAggrRules, ":memory:",
person_properties=list(gender="<unknown>"))
add_booklet(db, verbAggrData, "agg")
#> no column `person_id` provided, automatically generating unique person id's
#> $items
#> [1] "S1DoCurse" "S1DoScold" "S1DoShout" "S1WantCurse" "S1WantScold"
#> [6] "S1WantShout" "S2DoCurse" "S2DoScold" "S2DoShout" "S2WantCurse"
#> [11] "S2WantScold" "S2WantShout" "S3DoCurse" "S3DoScold" "S3DoShout"
#> [16] "S3WantCurse" "S3WantScold" "S3WantShout" "S4DoCurse" "S4DoScold"
#> [21] "S4DoShout" "S4WantCurse" "S4WantScold" "S4WantShout"
#>
#> $person_properties
#> [1] "gender"
#>
#> $columns_ignored
#> [1] "anger"
#>
add_item_properties(db, verbAggrProperties)
#> 4 item properties for 24 items added or updated
f=fit_enorm(db)
pv_M=plausible_values(db,f,(mode=="Do")&(gender=="Male"))
pv_F=plausible_values(db,f,(mode=="Do")&(gender=="Female"))
oldpar = par(mfrow=c(1,2))
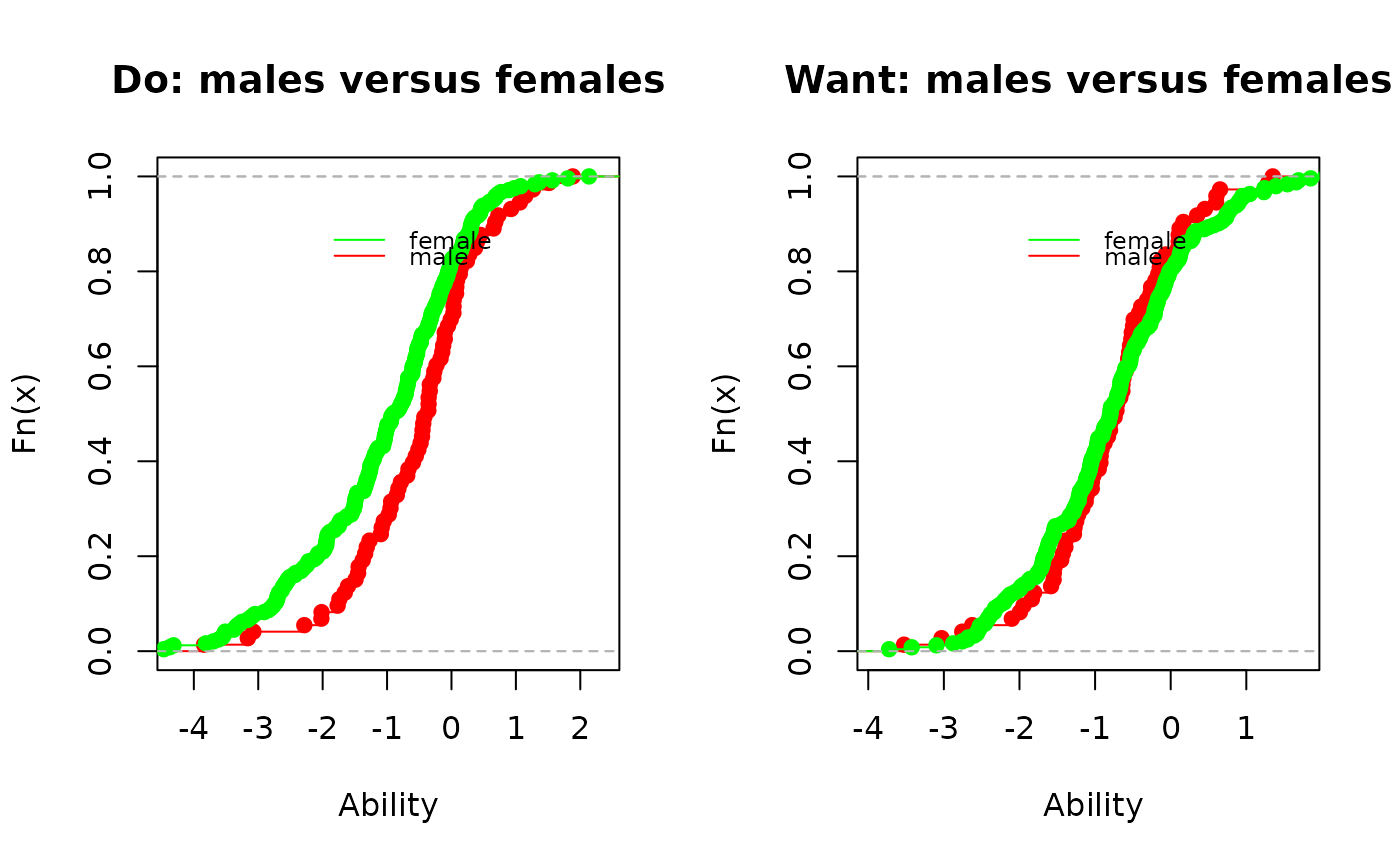
plot(ecdf(pv_M$PV1),
main="Do: males versus females", xlab="Ability", col="red")
lines(ecdf(pv_F$PV1), col="green")
legend(-2.2,0.9, c("female", "male") ,
lty=1, col=c('green', 'red'), bty='n', cex=.75)
pv_M=plausible_values(db,f,(mode=="Want")&(gender=="Male"))
pv_F=plausible_values(db,f,(mode=="Want")&(gender=="Female"))
plot(ecdf(pv_M$PV1),
main="Want: males versus females", xlab=" Ability", col="red")
lines(ecdf(pv_F$PV1),col="green")
legend(-2.2,0.9, c("female", "male") ,
lty=1, col=c('green', 'red'), bty='n', cex=.75)
 par(oldpar)
close_project(db)
par(oldpar)
close_project(db)